Teoría de Grafos

Para comenzar a diseñar un Aula Virtual en la nube se necesitan conocer algunos conceptos básicos sobre Teoría de Grafos y luego ir profundizando en la medida que se avanza. Un grafo es un conjunto de vértices (nodos) unidos por aristas. Gráficamente, los vértices son puntos y las aristas son líneas que los unen. La teoría de grafos permite representar y resolver matemáticamente muchos problemas de la vida cotidiana. Como una primera aproximación vamos a considerar como nodos los contenidos de una asignatura para establecer los caminos entre ellos. Cada arista puede representar el tiempo, el número de actividades aprobadas, la nota necesaria para pasar de un tema a otro, etc.

En el siguiente ejemplo se puede observar el diseño de una asignatura completa en la nube. En Educación Híbrida resulta más sencillo como se explicó en el Taller. Los nodos identificados con letras representan contenidos y las aristas la cantidad de tareas aprobadas para acceder. Los estudiantes deben recorrer todos los nodos. A partir de una evaluación diagnóstica, en el nodo de Entrada se define la primer arista a seguir y el número de actividades de nivelación a completar correctamente. Intuitivamente se necesita armar una matriz de 8 filas por 8 columnas para visualizar los caminos posibles y la cantidad de actividades diseñadas que conforman el Aula Virtual. A medida que comience a trabajar en el tema le surgirá la necesidad de contar con herramientas de la matemática condición suficiente para aprender con motivación y sentido práctico.

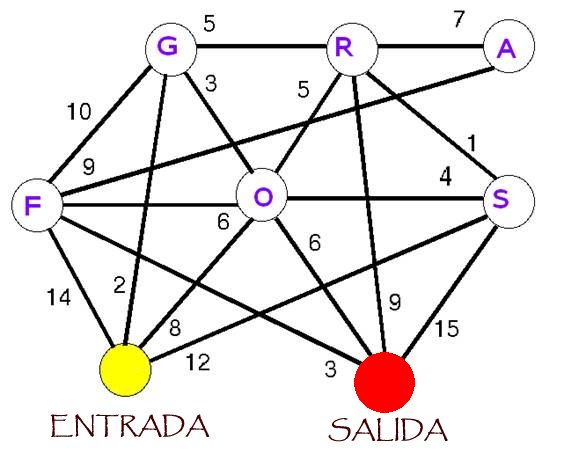
Consignas:

1. Analice si es posible recorrer el diagrama sin pasar dos veces por el mismo nodo. Si quiere saber la respuesta, vea la conferencia que sigue.
2. Intuitivamente ¿Aplica la Teoría de Grafos cuando organiza los contenidos y actividades de su asignatura?

El video que sigue contiene información para iniciarse en la Teoría de Grafos:

Referencias

Alsina, Claudi. Mapas del metro y redes neuronales: la teoría de grafos. Barcelona: RBA, 2011

Vieites Rodríguez, Ana María, et. al. Teoría de grafos. Ejercicios y problemas resueltos. Madrid: Paraninfo, 2014

Opt-out complete; your visits to this website will not be recorded by the Web Analytics tool. Note that if you clear your cookies, delete the opt-out cookie, or if you change computers or Web browsers, you will need to perform the opt-out procedure again.

You may choose to prevent this website from aggregating and analyzing the actions you take here. Doing so will protect your privacy, but will also prevent the owner from learning from your actions and creating a better experience for you and other users.

You are not opted out. Uncheck this box to opt-out. You are currently opted out. Check this box to opt-in.

The tracking opt-out feature requires cookies to be enabled.